Pendulum vs Metronome: Useful metaphors, bad physics”

Introduction
[The Pendulumic vs Metronomic Metaphors]{/inside-the-steps/pendulemic-and-metronomic-metaphors-debunked/pendulum-vs-metronomic-swing-basic-planar-three-link-leg-model}
The Pendulum metaphor in Dancing

Introduction Describing the curves that result from:

leg swing,
rise and fall,
sway. involves a lot of math and physics.

Back in the 1950's it was easier to use the terms "pendulum" and 'metronome' to describe swing. Those terms are sadly extremely simplistic and misleading resulting in dancers scratching their heads and saying "Wait, what??". Back in the 1950's it was easier to use the terms "pendulum" and 'metronome' to describe swing. Those terms are sadly extremely simplistic and misleading resulting in dancers scratching their heads and saying "Wait, what??". Worse still, those terms are baked into our industry. They are used extensively where the same metaphor is repeated (without change) across the internet, social media and books.

The snag: when we ask how these terms map onto Sway and Rise & Fall, the explanations almost always slide back to props and metaphors — a pendulum swing and for rise–fall and a metronome for sway — without a physical model behind them. As simplistic metaphors, they’re handy; as mechanics, they’re misleading and totally incorrect physics.

It's time to retire Metronomes and Pendulums before they confuse more dancers.

So we produced a simple animation showing a 'shoe' attached to a pendulum (and yes, it does look like a golf club)

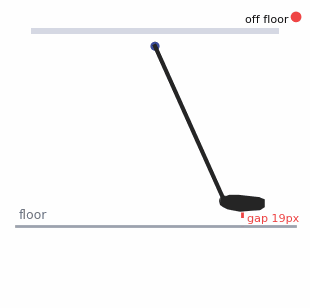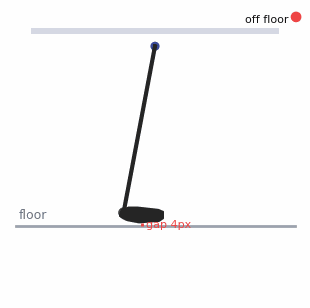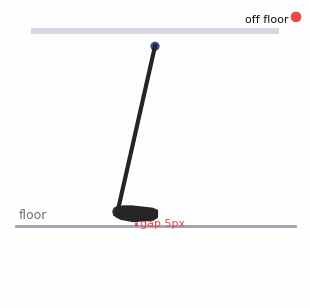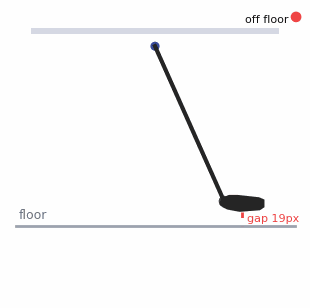Pendulum foot not contacting floor (gap indicator) Simple pendulum: a neat physics toy, but not how legs actually work.

This is pendular swing and it's just not something we use in Ballroom Dancing since the pivot point will move in any combination of up, down, left, right, forward or back. *What it doesn't do is stay in one place as required by the 'pendulum metaphor'.

And here's the "pendulum metaphor" math

Equation of motion (with optional damping \(b\)):
\(\theta''(t) + b\,\theta'(t) + \dfrac{g}{L}\, \sin\theta(t) = 0\)

Small-angle approximation \((\sin\theta ≈ \theta)\):
\(\theta(t) ≈ \theta \, \cos( \sqrt(\dfrac{g}{L})\, t + phi )\)
\(T_0 = 2π\, \sqrt(\dfrac{g}{L})\)

Large-amplitude period correction (\(θ\) in radians):
\(T ≈ T_0\) \(\,( 1 + \dfrac{1}{16}\,\theta^2 + \dfrac{11}{3072}\,\theta^4 + ... )\)

Screen coordinates (pivot at (x_p, y_p))
\(x(t)\) = \(x_p\) + \(L\, \sin(\theta(t))\)
\(y(t)\) = \(y_p\) + \(L\, \cos(\theta(t))\)

Given that the leg is really 3 independent pendulums:

thigh attached to the hip pivot point
shin connected to the thigh at the knee
foot connected to the shin at the ankle
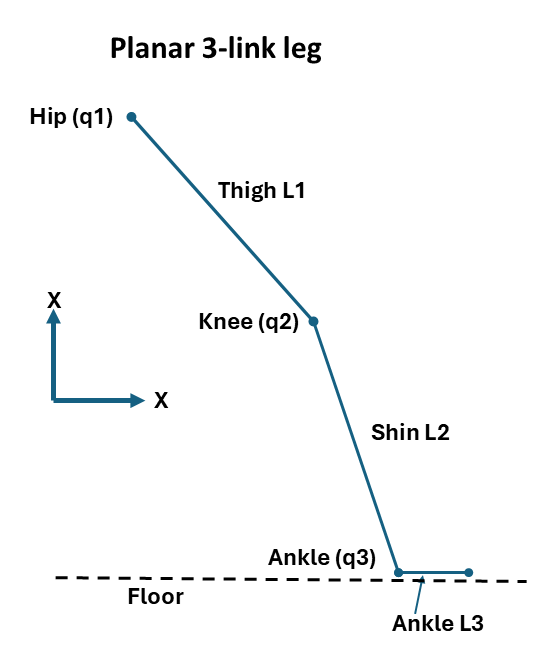things get a lot more complicated as there are 3 individual pendulum and metronome pivot points, \(q1, q2, q3\) and we dive a lot deeper here.

Here is an animation of a leg extension for a heel lead: (Click on the image to start the animation)

The Good News is...

... that there is almost no point in calculating all that for practical dancing (although math is fun).

“Pendular Rise and Fall”

You could easily use a visual metaphor of a pole leaning against a wall to describe pendulum and metronomic swing.

Is often presented as the engine of Rise & Fall, especially in Waltz. The implicit (and sometimes explicit) assumption is a sinusoidal rise and fall curve. It isn’t. In this section we showed that Rise & Fall is not a sine wave, and trying to dance it as one is virtually impossible and breaks the 'least action' that governs our dancing. This is the plot of Rise and Fall for Waltz:

Graph of rise and fall in ballroom dance

and it's obviously not a sine wave. It's also obvious that this cannot be produced with the 'pendulum' metaphor.

The 'Pendulum metaphor' has no foundation in physics and is dubious at best as teaching / explanatory technique since it has little to no relevance to what has to happen.

“Metronomic Swing”

A term usually invoked for Sway, sometimes split into “Technical Sway” and “Upper Body Sway”. The implicit picture is a sine wave of lateral tilt driven by rotation. Again: it's not a sine wave, and not realistically danceable as one.

Metronomes describe an arc from a fixed point using a fixed length rod which is exactly what we don't have in dancing.

Dancing is about travel and movement

Dancing is about travel and movement to create changes in shape. If we divide time into teeny little increments (\(\dfrac{dx}{dt}\), \(\dfrac{dy}{dt}\) and \(\dfrac{dz}{dt}\)) where almost no motion is occurring it's possible to use the metronome and pendulum metaphors.

The “pendulum” and “metronome” metaphors are not just incomplete, they are wrong. They depend on fixed pivots and passive sinusoidal swings — features that do not exist in dancing. Persisting with them creates confusion, wasted practice, and broken biomechanics. What actually drives Rise & Fall and Sway is controlled travel, jointed limb dynamics, and balance management, not props on strings. We should stop teaching with gimmicks and start teaching from science.