Planar 3-link leg (1 dimension)
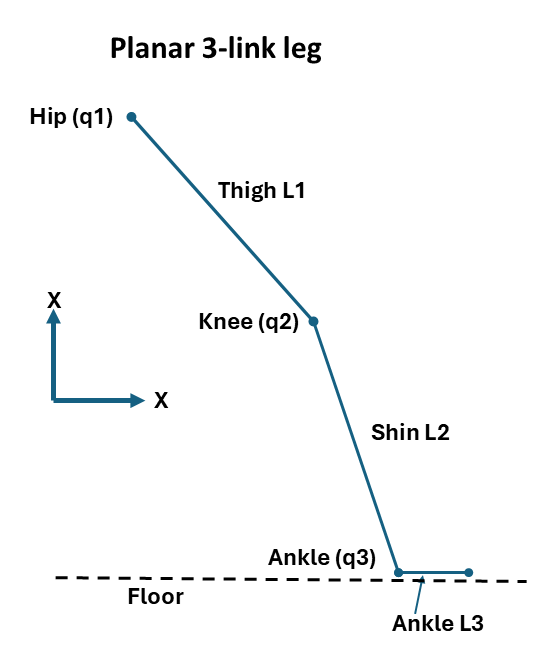
Generalized coordinates:
\(q = [q1,\, q2,\, q3]\,^\tau\)
where:
- \(q1\) is the hip,
- \(q2\) is the knee
- \(q3\) is the ankle (all angles are in radians)
Dynamics (Lagrange/Euler form): \(M(q) \, \ddot{ q} + C(q,\dot{ q}) \, \dot{ q} + G(q) = \tau\)
Where: \(M(q)\) 3×3 positive-definite inertia matrix (link masses inertias) \(C(q,\dot{ q})\) Coriolis/centrifugal terms (velocity-dependent) \(G(q)\) gravity torques \(\tau\) joint torques \([\tau_{hip}, \tau_{knee}, \tau_{ankle}]\,^\tau\) (muscle/partner/assist)
Notes: • If \(\tau\) ≈ 0 and motions are small, each link behaves locally like a physical pendulum about its joint—BUT links remain coupled via \(M\) and \(C\), and knee/ankle pivots move. • In stance, foot–floor contact imposes constraints → inverted-pendulum over the COP (Center Of Pressure) path.
The equation:
\[ M(q)\ddot{ q} + C(q,\dot{ q})q+G(q)=τ\]
is the standard form of robot manipulator / multi-link dynamics. Here’s the breakdown:
Where:
- \(q\) vector of joint angles (for the leg: hip, knee, ankle).
- \(\ddot{ q}\) joint accelerations.
- \(M(q)\) the mass/inertia matrix (depends on link lengths, masses, orientations). It couples all the joints together.
- \(C(q,\dot{ q})\dot{ q}\) the Coriolis and centrifugal forces, velocity-dependent “extra pushes” that appear whenever links are moving.
- \(G(q)\) gravity torques (how gravity tries to rotate each joint).
- \(\tau\) (Tau) applied torques at the joints (muscles or external forces).
Why it’s important
- It’s the canonical dynamic equation for any multi-link chain (robot arm, human leg, etc.).
- Each piece has clear meaning:
- \(M\) = how hard it is to move.
- \(C\) = weird cross-couplings when you move more than one joint.
- \(G\) = gravity always pulling you down.
- τ = the torque you need to apply to achieve motion.
In dancing terms
- If τ=0 (no muscle/partner input), the leg would swing like a bunch of linked pendulums.
- In reality, \(\tau ≠ 0\) you’re constantly injecting torque to shape the path.
That’s why the pendulum/metronome metaphor breaks down: the pivots are moving, the inertia terms couple everything, and gravity’s torque is always being “fought” or redirected.
“The leg is governed by coupled second-order equations: inertia + velocity-coupling + gravity = muscle torques. The pendulum picture ignores all but gravity, so it’s a cartoon, not a model.”
Planar 3-link leg dynamics (block form)
Let (hip, knee, ankle respectively).
\[ q=\begin{bmatrix} q_1\\ q_2\\ q_3 \end{bmatrix},\quad \dot {q}=\begin{bmatrix} \dot {q_1}\\ \dot {q_2}\\ \dot{ q_3} \end{bmatrix},\quad \ddot {q}=\begin{bmatrix} \ddot {q_1}\\ \ddot {q_2}\\ \ddot {q_3} \end{bmatrix}, \quad \tau=\begin{bmatrix} \tau_1\\ \tau_2\\ \tau_3 \end{bmatrix} \]
The standard manipulator form:
\[ M(q)\,\ddot{ q} \;+\; C(q,\dot{ q})\,\dot{ q} \;+\; G(q) \;=\; \tau \]
In blocks
\[ \underbrace{\begin{bmatrix} M_{11} M_{12} M_{13}\\ M_{21} M_{22} M_{23}\\ M_{31} M_{32} M_{33} \end{bmatrix}}_{M(q)} \! \underbrace{\begin{bmatrix} \ddot {q_1}\\ \ddot {q_2}\\ \ddot {q_3} \end{bmatrix}}_{\ddot {q}} \;+\; \underbrace{\begin{bmatrix} C_{11} C_{12} C_{13}\\ C_{21} C_{22} C_{23}\\ C_{31} C_{32} C_{33} \end{bmatrix}}_{C(q,\dot {q})} \! \underbrace{\begin{bmatrix} \dot {q_1}\\ \dot {q_2}\\ \dot {q_3} \end{bmatrix}}_{\dot {q}} \;+\; \underbrace{\begin{bmatrix} G_1(q)\\ G_2(q)\\ G_3(q) \end{bmatrix}}_{G(q)} \;=\; \underbrace{\begin{bmatrix} \tau_1\\ \tau_2\\ \tau_3 \end{bmatrix}}_{\tau} \]
Per-joint components
\[ \begin{aligned} \text{Hip: } M_{11}\,\ddot{q_1} + M_{12}\ddot{ q_2} + M_{13}\ddot {q_3} \;+\; \sum_{j=1}^3 C_{1j}\dot {q_j} \;+\; G_1(q) \;=\; \tau_1\\ \text{Knee: } M_{21}\ddot {q_1} + M_{22}\ddot {q_2} + M_{23}\ddot {q_3} \;+\; \sum_{j=1}^3 C_{2j}\dot {q_j} \;+\; G_2(q) \;=\; \tau_2\\ \text{Ankle: } M_{31}\ddot {q_1} + M_{32}\ddot {q_2} + M_{33}\ddot {q_3} \;+\; \sum_{j=1}^3 C_{3j}\dot {q_j} \;+\; G_3(q) \;=\; \tau_3 \end{aligned}\]
State-space (compact)
\[ x=\begin{bmatrix} q\\ \dot{ q} \end{bmatrix},\qquad \dot{ x} \;=\; \begin{bmatrix} \dot{ q}\\[3pt] M(q)^{-1}\big(\tau - C(q,\dot{ q})\dot{ q }- G(q)\big) \end{bmatrix}\]
In English
So in plain English:
- M = how hard it is to accelerate links (mass/inertia).
- C = the weird extra forces from moving joints (velocity coupling).
- G = gravity’s ever-present pull.
- τ = the “steering wheel” rotation you apply with muscle and partner forces.
TL;dr Legend
- \(M(q)\): inertia/coupling matrix (symmetric, positive-definite).
- \(C(q,\dot{ q})\dot{ q}\): Coriolis/centrifugal velocity couplings.
- \(G(q)\): gravity torques.
- \(\tau\): applied joint torques (muscle/partner/assist).
Full Legend
\(M(q)\) Inertia (Mass) Matrix
- What it is: A 3×3 symmetric, positive-definite matrix. Each entry reflects how joint accelerations produce torques, including cross-coupling.
- Why it matters: Moving the thigh doesn’t just load the hip; it changes what the knee and ankle “feel.” The inertia matrix captures all those link–link interactions.
- In dance terms: It explains why flicking a leg feels different depending on whether the rest of the leg is free or braced — the distribution of mass couples the joints.
\(C(q,\dot{ q})\dot{ q}\) Coriolis Centrifugal Forces
- What it is: A vector of terms quadratic in velocity. They represent “fictitious” forces that appear when links rotate.
- Why it matters: Even if muscles do nothing, moving joints create extra pushes and pulls elsewhere. That’s why swinging the thigh makes the shank and foot want to whip.
- In dance terms: This is the “lag and catch” you feel when the shank and foot follow a thigh swing - not magic, just Coriolis/centrifugal coupling.
\(G(q)\) Gravity Torques
- What it is: The torque at each joint required to hold the leg still against gravity at configuration \(q\).
- Why it matters: Gravity is always tugging each link downward. Depending on posture, more torque is needed at hip, knee, or ankle.
- In dance terms: It’s the load you feel holding a développé or extension — the joint torques required just to “park” the leg in space.
Applied Torques (\(\tau\))
- What it is: The vector of actual joint efforts (muscles, tendons, or external partner forces).
- In dance terms: This is you — the muscle input shaping swing, sway, and balance.